黎明期の開発事情

私が初めてパソコンを購入した頃は、MS-DOSが広く普及する少し前でしたので、OSというものを使用していませんでした。決して存在しなかった訳ではありませんが、N88BASICが標準で用意されていましたので、別途OSを購入しなくても済んだというのが実状です。 N88-BASICは、厳密にはOSには分類されないのかも知れませんが、OSが担う機能を持っていましたので、それで充分でした。

前身であるPC-88シリーズからBASIC言語が広まっていましたので、PC-98シリーズでもそれを踏襲した訳ですが、これらはN88BASICと呼ばれ、ROM-BASIC・Disk-BASIC・DOS版BASICの3つがありました。ちなみに、QuickBASICとかVisualBasicなどは、広く知られたBASICの言語仕様を引き継いだもので、これよりずっと後のものと考えて下さい。

パソコン起動時、フロッピーディスクやハードディスクなどからブート可能なものを探し、もしもない場合には「How many file(0-15)?」と表示されるのですが、これがROM-BASICの正体です。この画面からBASICプログラムを打ち込んで実行することができます。

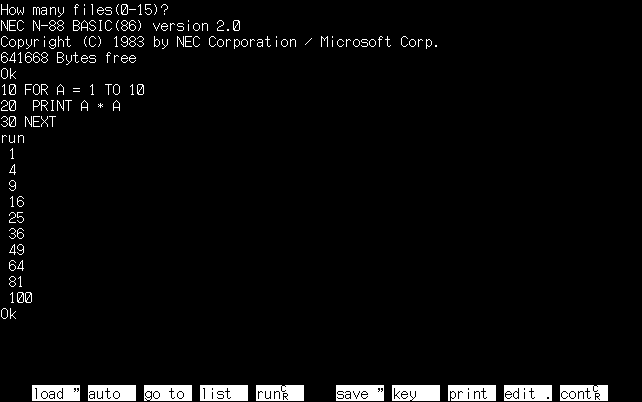
ROM-BASICでは、通常プログラムの保存先がないため、メモリ上のプログラムは電源を切ると消えてしまいます。対処方法として、例えばRS-232CでCOMポート接続して送受信などすればファイルの読み書きはできますが、私はそこまで使った経験はありませんので、ここでは省略させて頂きます。実質的にはパソコン付属のDisk-BASICを使うことになります。システムディスクから起動すると、こんな画面が立ち上がります。

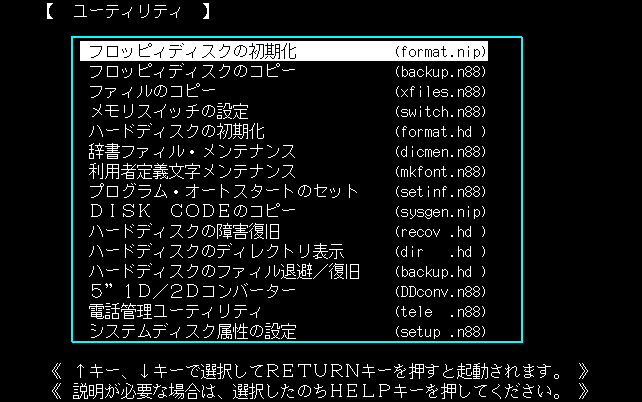
マシンの設定・ディスクの初期化やコピーなど、今ではOSが担う機能まで組み込まれていることがわかります。
裏事情についても少し触れておきますと、PC-98の実機はもう手元にありませんので、画面イメージ取りなどはエミュレータを使用しています。
そもそも、将来Disk-BASICが使えるなどは夢にも思わなかったのですが、媒体をただ捨てるのは勿体ないので、実機があればいつでも復元できるようにはしておこう、という程度の思いで残したシステムディスクのイメージファイルでした。エミュレータを使い始めた頃、Disk-BASICは動きませんでしたが、バージョンアップでいつの間にかサポートされていたのです。わざわざ古い機能をサポートしてくれるようになるとは願ってもいませんでした。今生の別れをした友人に再び出会えたような気分で、この画面が立ち上がった時にはそれはそれは感動しました。

当時の私は、5インチのフロッピーディスク媒体を購入して来て、初期化・システム転送をした状態のものを作り、ここから起動して自分のBASICプログラムを保存して使っていました。これが私の最初の開発環境です。

この環境でしばらくの間は何の不自由も感じなかったのですが、ハードディスクが普及してくると、MS-DOSの導入が当たり前になって来ます。 MS-DOSはHD起動、Disk-BASICはFD起動と使い分けていましたが、毎回マシンの再起動が必要になるのが面倒と感じ始めた頃、 MS-DOS版のBASICというものが存在することを知り、そちらへ切り替えを行いました。 Disk-BASICで作成済みのプログラムは、アスキーセーブすれば、MS-DOSの標準コマンド「FILECONV.EXE」で MS-DOSファイルに変換できますので、ちょっとしたサンプルプログラムや不要なテストプログラムなどを除いてほとんどのソースはMS-DOSにコンバートしました。
この切り替えを機に、私の中ではDisk-BASICを利用することはなくなりました。思えば短いDisk-BASIC開発期間ではありましたが、私の原点とも言える大切な体験でした。

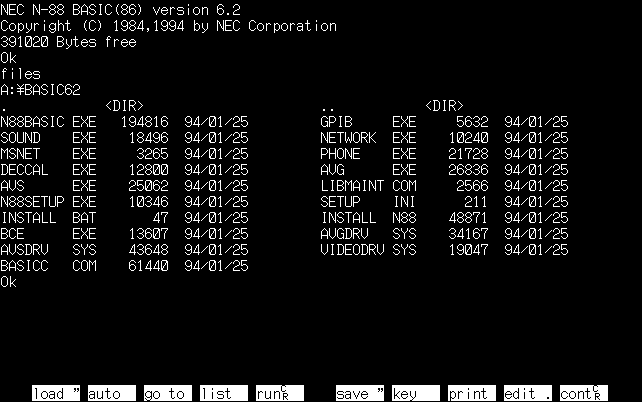
DOS版BASICでもうひとつ特筆すべきことがあります。確か別売りだったと記憶していますが、BASICC.COMというコンパイラが含まれたことです。これにより「BASIC」＝「インタプリタ型の開発環境」という概念に少し変化が起きました。
インタプリタとは、ソースファイルを一行ずつ解読しながら実行するタイプのもので、コンパイルという手間がなく、エラーが起きた行で止まるため、エラー箇所を直して継続実行ができる、という手軽さが売りでしたが、実行速度が遅いという致命的な欠点がありました。コンパイラの登場により、開発途中はインタプリタの利点を活かして、ある程度出来上がったらコンパイルする、というスタイルが確立されました。コンパイルを実施すると、ソースファイル○○○○.BAS以外にも実行ファイル○○○○.EXEが作成されるようになりますが、これは「N88BASIC.LIB」という専用のライブラリさえあれば開発環境は不要で、プログラムの公開をしてもソースは秘密にできるなど、それまでのBASICの開発環境とは一味違うものになっていったように思います。当時、EXEファイルといえばMS-DOSに付属するシステムコマンドという印象が強かったのですが、 BASICC.COMのようなコンパイラを使えば、自分で名前を付けたEXEファイルを作ることができ、これは非常に感動的な体験でした。EXEファイルは、MS-DOS上で実行可能なバイナリ形式の標準であり、自作のプログラムを「完成品」として配布できることに強い魅力を感じました。ユーザは全てプログラマでもあるという時代から、開発者と利用者という立場の違いがこうやってできていったのかも知れません。

BASICC.COMで生成される実行ファイルは、完全な機械語ではなく、Pコードと呼ばれる中間コードを使っています。これは仮想マシン上で実行される形式で、インタプリタよりは高速に動作しますが、純粋なネイティブコードと比べると処理速度はやや劣ります。それでも、コンパイラ型の利点を世に知らしめた功績は大きいと思っています。より本格的なプログラムを求めて、ネイティブコードを出力するCコンパイラなどに移行していくことになります。

◆私がパソコンを使い始めた理由

唐突ですが、あなたががパソコンを使い始めた理由はなんですか？「ただ何となく」とか、「自宅や学校や職場にあったから」などという人は21世紀になってからパソコンを使い始めたのではないでしょうか。この当時はパソコンの値段も高く普及率も低かったのですが、そんな時代から敢えてパソコンを使う人というのは、何かしらの明確な目的があった人が多かったのではと思います。

手元に正確な統計がある訳でもないので、あくまで私の感覚ですが、パソコンを使い始める理由としてはやはりゲーム目的という人が多かったかなと思います。あとはワープロをしたいからと導入したがこれならワープロ専用機の方が使い易かったではないかと気づいたり、コンピュータ・グラフィックがしたいけどまともな絵など書けなかったり、コンピュータ・ミュージックをしたいけどそもそも音が出すのにこんなに金がかかるのかと嘆いたり、そんな時代でした。

私の場合は、実は3次方程式を解くためだったんです。「何言ってんの、この人？」と思われるかも知れませんが、事実なので仕方ありません。もう少し汎用的な言い方をすれば「構造計算」ということになります。職務上、建築現場の土留めの計算を行わないといけなかったのですが、その許可申請書類に構造計算書を付ける必要がありました。

この辺りは、眠たい話しになりますので、興味ない方は寝てて下さい、あとで起こします。
※本当に眠られても困るので、そんな方はここをクリックして下さい。眠い話しを飛ばせます。

構造力学では「構造物の静定はモーメントの総和がゼロ」ということになるのですが、モーメントは剪断力を変位で積分したもの、剪断力は荷重を変位で積分したものになります。荷重には、集中荷重・等分布荷重・偏分布荷重があり、水圧・土圧などは偏分布荷重なのですが、これは荷重が変位の1次式になります。ということは剪断力は変位の2次式、モーメントは変位の3次式となります。土圧・水圧がかかる構造物の静定、モーメントの総和ゼロの式を立てると、どうしても3次方程式を解くことが必須となる訳です。

ところで皆さん、3次方程式ってどうやって解きますか？

高校の数学で3次方程式を解いたような記憶がありますが、大体こんな方法でした。
※ネット上より引用。

「頑張って解を一つ探す」って言われても、実務で解く3次方程式はそんなに甘くなく、通常は見つかりません。ひとつ解を見つけるのが前提ってことは、3次方程式の中で限られた条件のものを2次方程式の手法を使って解いただけで、これでは3次方程式そのものを解いたことにはならないってことですよね（苦笑）。学校で習う数学が実務では如何に役に立たないか痛感する実例です。

どうしたらいいのか悩みましたが、同期入社に構造計算に詳しい奴（仮名：野崎）がいまして、彼に聞いたところ「BASICでプログラムを組んで解いている」とのことでした。

「y = ax^3 + bx^2 + cx +d」の計算式で、a, b, c, d の係数は決まっていますので、x = 0, 1, 2, 3と代入して行きyの値を調べます。例えば2から3に変わった時yの正負が逆になれば、この間に解が存在するので、今度は x = 2.0, 2.1, 2.2 と代入してyの正負が逆転する値を求めます。これを求めたい精度の桁まで繰り返して行くという解き方でした。

「なるほど、流石」と思ったのですが、この方法には2つの問題がありました。
①ひとつは正の最小値しか取れないこと、
②もうひとつは、係数によってはひとつも見つからない場合もあることです。
どれだけ掘るかを計算するのに虚数解やマイナス値が出ても意味がないし、正の実数解が複数あれば小さい方でよい、という条件のため、それで問題ないことが多いので①は目をつぶるとします。
問題は②の方です。
最初の増分値の間に（例えば2から3の間に）2つの解があるような場合に見つけられません。几帳面で真面目な彼は、問題が起こる都度、ロジックを工夫して何とか対処していたそうです。そういう手間がかるデメリットを差し引いても実務上役立つツールにはなっていましたので、それはそれで参考にはなったのですが、几帳面でもなく真面目でもない私には（自分で言う？）どうも納得がいきませんでした。

そんな時、「カルダノの解法」と呼ばれる3次方程式の解の公式があることを知ります。実際に発見したのはカルダノではなくタルタリアですが、この辺りの詳しい話しは数学の専門書に譲るとして、私はこの公式をそのまま解くようなプログラムを作って見ました。これで複素数の範囲で3つの解が見つかるようになりました。仕事もスムーズに進められるようになり、構造計算そのものに自信を持てました。

さてここで、眠っていた皆さん、そろそろ目を覚まして下さい（と律儀に起こす）。

最初に多少苦労してでも後から楽になる・便利になる面白さ、一度作ったものを改善する面白さ、私はすっかりプログラミングの虜になってしまいました。

「カルダノの解法」が出来て、しばらくすると今度は「ヘロンの公式」も作ることになります。土地の広さを図ったり、その図面を書いたりするのに平板測量という方法を使うのですが、どんなに複雑な地形でも直線で区切られていれば三角形の集まりと見なすことができ、その各辺の長さを測れば、個々の三角形の面積が求められます。あとは各三角形の面積の総和を求めればいいわけです。
この時、3辺の長さから面積を求める計算が必要となりますが、ここでヘロンの公式が役立ちます。公式の詳細は数学関連のサイト等をご参照下さい。

実測した3辺なら必ず三角形として成立するのですが、入力ミスなどした時に変なエラーが出ることがあります。例えば「任意の2辺の和が残りの1辺より大きい」を満たさない場合、 √の中が負になってエラーになります。こうしたケースを事前に検出して、ユーザーに「入力に誤りがあります」と伝えられるようにしたのです。自分さえ使えればよかったので放っておくという選択肢もありましたが、より完成度を高めたいという気持ちが勝ったようです。
自作ツールながら市販アプリのクオリティーに近づける面白さもこの頃学びました。もちろん市販アプリには完成度や信頼性の高さという利点もありますが、自分の業務フローにぴったり合ったツールを自作できることに、私は大きな喜びを感じていました。

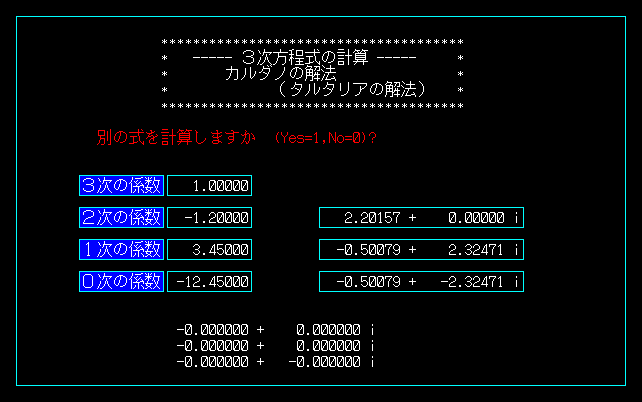
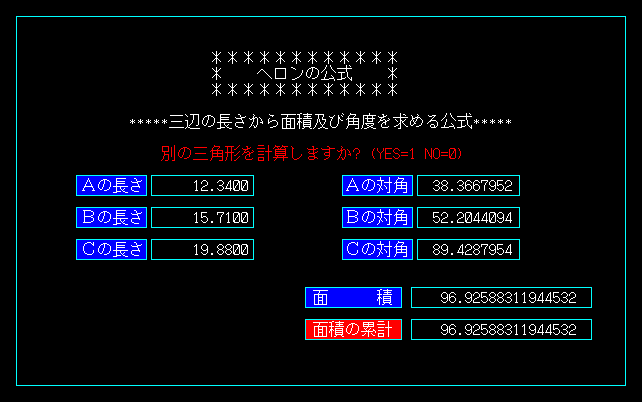
私がよく使う数学の公式がこの2つですが、このソースを見たい方はこちらからダウンロードして下さい。
タイムスタンプを見ると1992年、今から27年ほど前になりますが、昔の拙いソースを見られるのは小学生の頃に書いた作文を読まれるみたいな感じで恥ずかしい思いがします。まだプログラマとして非力だったからなのか、構造化プログラミングが難しいBASICという言語だからなのか、恐らくその両方なのでしょう。当時の私はまだこんなもんでした。

戻る